5. Examples
5.1. Poiseuille Flow
We define the simulation domain for the Lattice Boltzmann Method (LBM). In this example, we choose a resolution of 30×30×30. Periodic boundary conditions are applied along the XX and YY axes, while the ZZ axis remains non-periodic.
do_domain:
- domain:
bounds: [ [0,0,0] , [0.1,0.1,0.1] ]
grid_dims: [ 30 , 30 , 30 ]
periodic: [ true, true, false ]
We apply two Neumann boundary conditions on the Z axis, (setting to (ux = 0, uy = 0, uz = 0)):
boundary_conditions:
- neumann_z_l:
U: [0.0,0,0]
- neumann_z_0:
U: [0.0,0,0]
An external force of (9.512485×10−5,0.0,0.0) is applied to drive the flow. The kinematic viscosity is set to 1e−3, and the average density is assumed to be 1000.
set_lbm_parameters:
- lbm_parameters:
Fext: [9.512485e-05,0.000000e+00,0.000000e+00]
nuth: 1e-3
The global parameters for this simulation include output frequency and the total number of iterations:
global:
simulation_paraview_freq: 100
simulation_end_iteration: 3000
The expected results should show the development of a fully developed Poiseuille flow profile along the Z axis, with velocity increasing towards the center and decreasing near the boundaries due to the imposed Neumann conditions.

5.2. Couette Flow
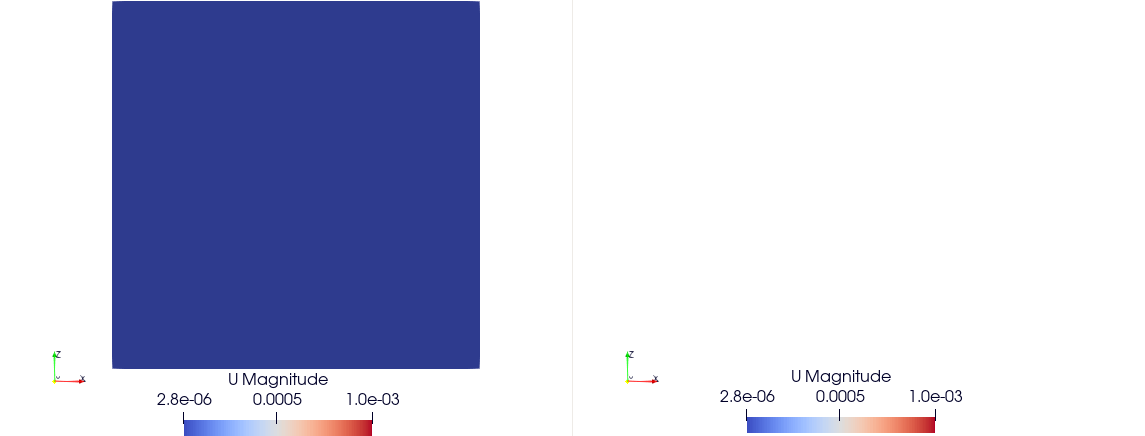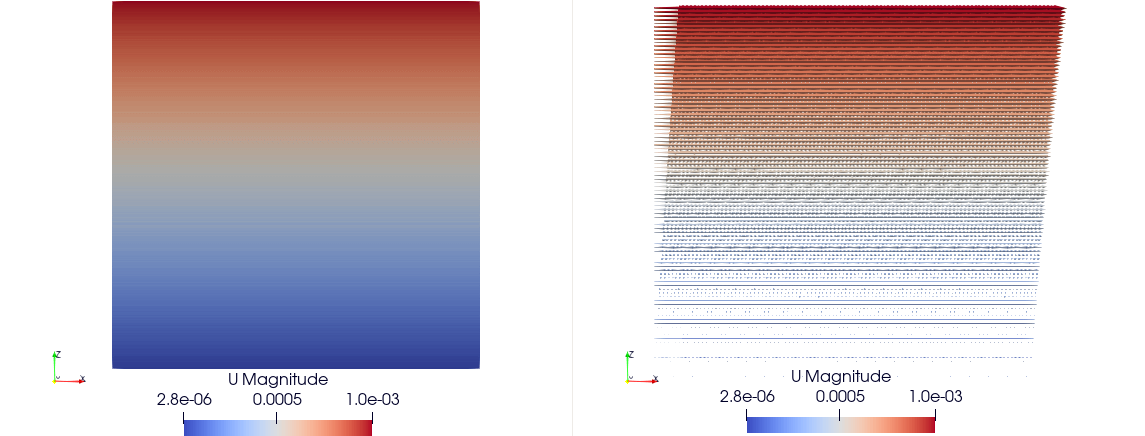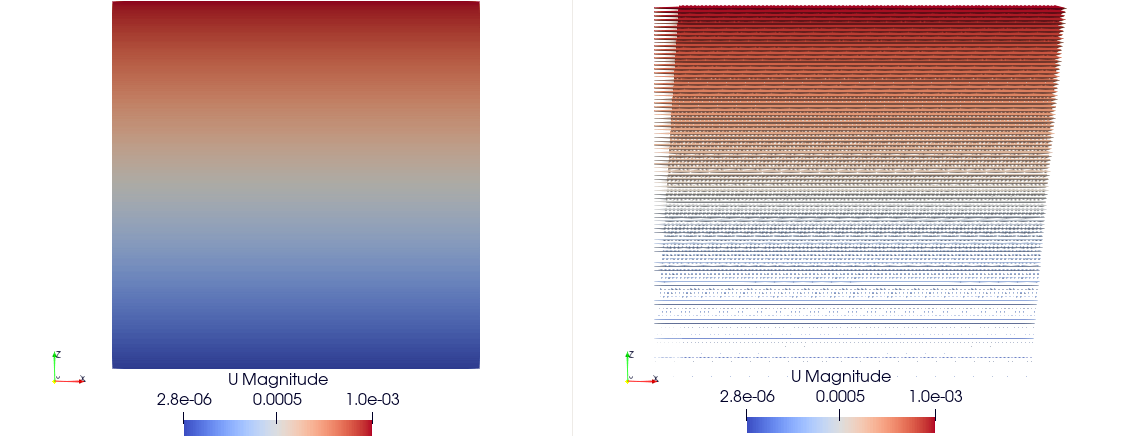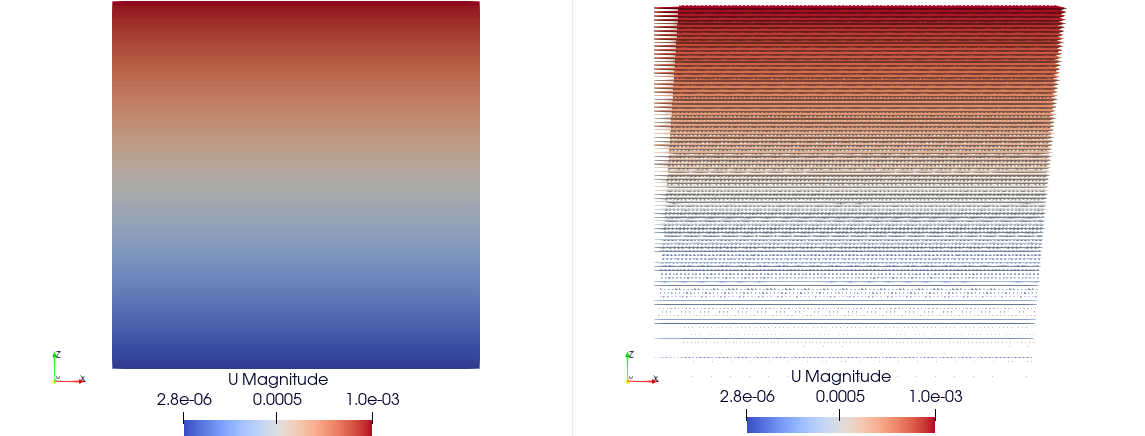
We define the simulation domain for the Couette flow using the Lattice Boltzmann Method (LBM). In this case, we set the resolution to 100×100×100, with periodic boundary conditions applied on the XX and YY axes, and non-periodic boundary on the ZZ axis.
do_domain:
- domain:
bounds: [[0,0,0],[0.1,0.1,0.1]]
grid_dims: [ 100 , 100 , 100 ]
periodic: [true, true, false]
We set the Lattice Boltzmann parameters with a kinematic viscosity (nuth) of 1e-2 and no external force applied (i.e., Fext = [0, 0, 0]).
set_lbm_parameters:
- lbm_parameters:
Fext: [0.000000e+00,0.000000e+00,0.000000e+00]
nuth: 1e-2
Boundary conditions are applied on the Z axis. On the lower boundary (neumann_z_l), the velocity is set to U = [0.001, 0, 0].
boundary_conditions:
- neumann_z_l:
U: [0.001,0,0]
The expected results will show a linear velocity profile along the Z axis, where the velocity increases linearly from the stationary bottom boundary to the top boundary with a constant shear rate, characteristic of Couette flow.
5.3. Cavity Flow
We define the simulation domain for the cavity flow using the Lattice Boltzmann Method (LBM). In this case, the resolution is set to 200×200×200, with non-periodic boundary conditions applied in all directions (XX, YY, and ZZ).
do_domain:
- domain:
bounds: [ [0,0,0] , [0.1,0.1,0.1] ]
grid_dims: [ 200 , 200 , 200 ]
periodic: [ false, false, false ]
We set the Lattice Boltzmann parameters, with no external force applied (i.e., Fext = [0, 0, 0]) and a kinematic viscosity (nuth) of 1e-4.
set_lbm_parameters:
- lbm_parameters:
Fext: [0.000000e+00,0.000000e+00,0.000000e+00]
nuth: 1e-4
The boundary conditions for the simulation are defined as follows:
Pre-streaming boundary conditions: The pre_bounce_back and cavity_z_l conditions are set, with a velocity of U = [0.0, 0.1, 0] applied on the lower Z boundary.
Post-streaming boundary condition: The post_bounce_back condition is applied on the other boundaries.
pre_stream_bcs:
- pre_bounce_back
- cavity_z_l:
U: [0.0, 0.1, 0]
post_stream_bcs:
- post_bounce_back
The expected results will show the development of a cavity flow pattern, where the fluid moves along the Z axis, influenced by the velocity set on the lower boundary. This is typical for cavity simulations, where the fluid is confined within a box.
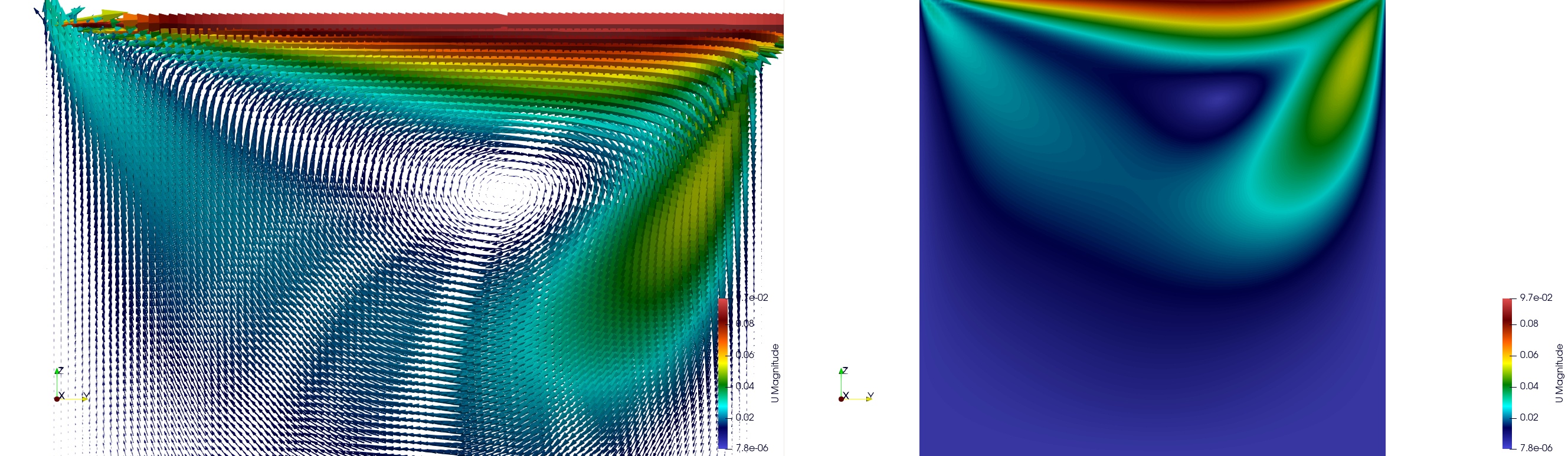
5.4. Cavity Flow with Wall Obstacle
This example simulates cavity flow using the Lattice Boltzmann Method (LBM) with a fixed obstacle (wall) in the middle of the domain. The domain resolution is 100×100×100, and non-periodic boundary conditions are enforced on all axes (XX, YY, and ZZ).
do_domain:
- domain:
bounds: [ [0,0,0] , [0.1,0.1,0.1] ]
grid_dims: [ 100 , 100 , 100 ]
periodic: [ false, false, false ]
No external force is applied (Fext = [0, 0, 0]), and the kinematic viscosity is set to 1e-4.
set_lbm_parameters:
- lbm_parameters:
Fext: [0.000000e+00,0.000000e+00,0.000000e+00]
nuth: 1e-4
Boundary conditions are applied as follows:
Pre-streaming:
pre_bounce_back applies bounce-back on walls.
cavity_z_l sets a moving lid on the lower Z boundary with velocity U = [0.1, 0.0, 0].
wall_bounce_back enables bounce-back condition for the internal obstacle.
Post-streaming:
post_bounce_back finalizes bounce-back conditions after streaming.
pre_stream_bcs:
- pre_bounce_back
- cavity_z_l:
U: [0.1, 0.0, 0]
- wall_bounce_back
post_stream_bcs:
- post_bounce_back
An internal obstacle is defined using the set_obstacles field. A vertical wall is placed at the center of the domain, slightly offset in the X-direction, spanning from Z = 0 to Z = 0.08.
set_obstacles:
- set_wall:
bounds: [[0.048,0,0],[0.052,0.1,0.08]]
The expected result is a modified cavity flow field with recirculation zones forming around the central wall obstacle, demonstrating how internal structures influence fluid dynamics in confined spaces.

5.5. Pressure-Driven Flow
This simulation demonstrates the effect of a strong pressure or density difference using the Lattice Boltzmann Method (LBM). The domain has a resolution of 100×100×100, with periodic boundary conditions along the Y axis, and closed boundaries in X and Z.
do_domain:
- domain:
bounds: [ [0,0,0] , [0.1,0.1,0.1] ]
grid_dims: [ 100 , 100 , 100 ]
periodic: [ false, true, false ]
No external force is applied. The kinematic viscosity is set to 1e-4.
set_lbm_parameters:
- lbm_parameters:
Fext: [0.000000e+00,0.000000e+00,0.000000e+00]
nuth: 1e-4
The pre-streaming boundary conditions include:
pre_bounce_back: standard no-slip boundary on external walls.
wall_bounce_back: bounce-back for internal structures.
pre_stream_bcs:
- pre_bounce_back
- wall_bounce_back
Two vertical internal walls are added near the center of the domain, one at the top and one at the bottom, leaving a gap in the middle. These walls obstruct flow and create more complex recirculation patterns.
set_obstacles:
- set_wall:
bounds: [[0.048,0,0.06],[0.052,0.1,0.1]]
- set_wall:
bounds: [[0.048,0,0],[0.052,0.1,0.04]]
A high-density region is initialized on the left-hand side using init_distributions with a coefficient of 1.5. This creates a pressure difference between the left and right sides of the domain, acting as the flow-driving mechanism.
set_distributions:
- init_distributions:
tmp_coeff: 1.5
bounds: [[0,0,0], [0.048,1,1]]
The post-streaming boundary condition is the standard post_bounce_back.
post_stream_bcs:
- post_bounce_back
The goal of this setup is to observe how a sharp pressure gradient (from the initialized distribution) drives flow across the domain.
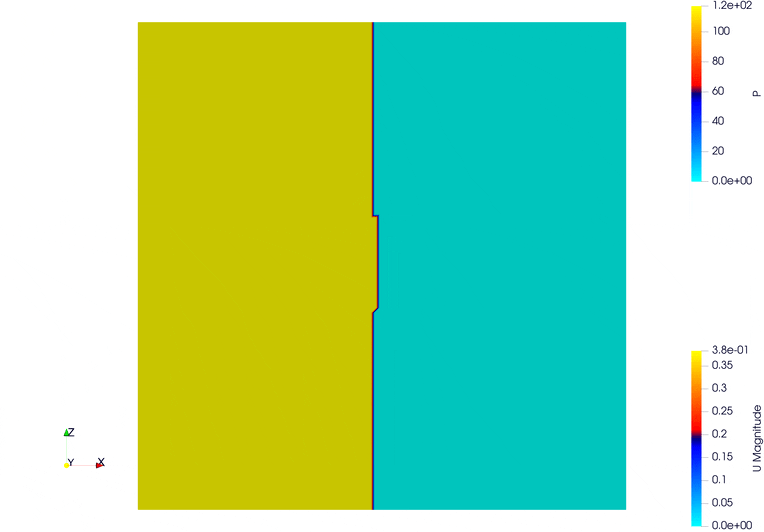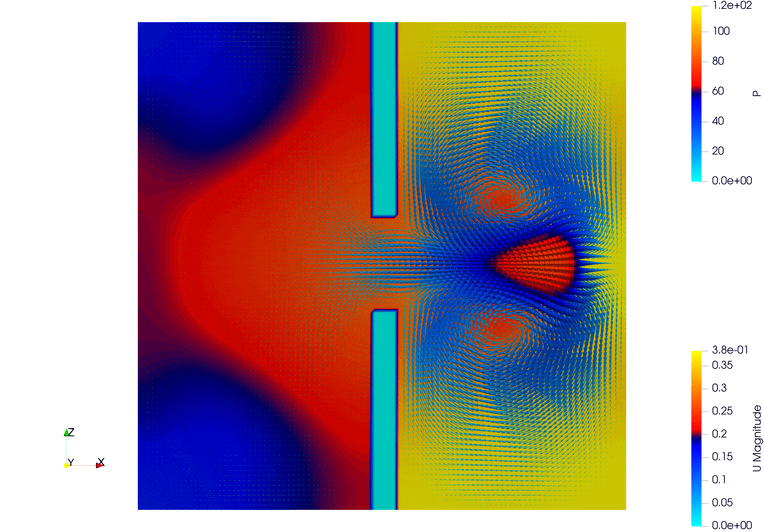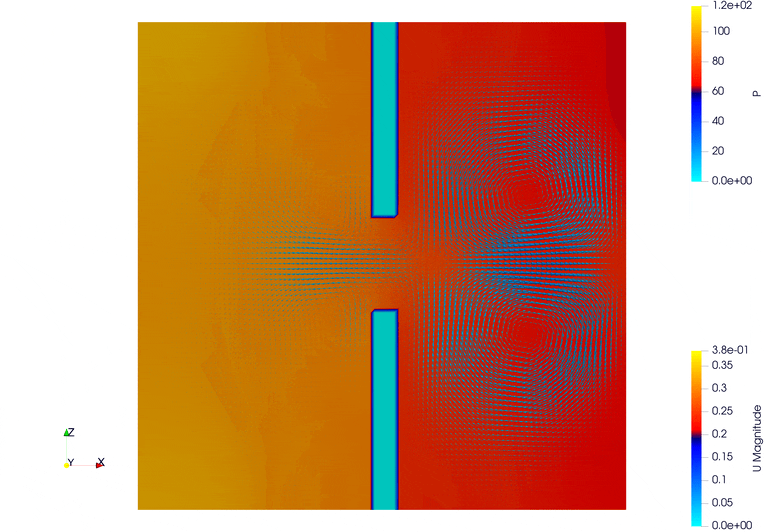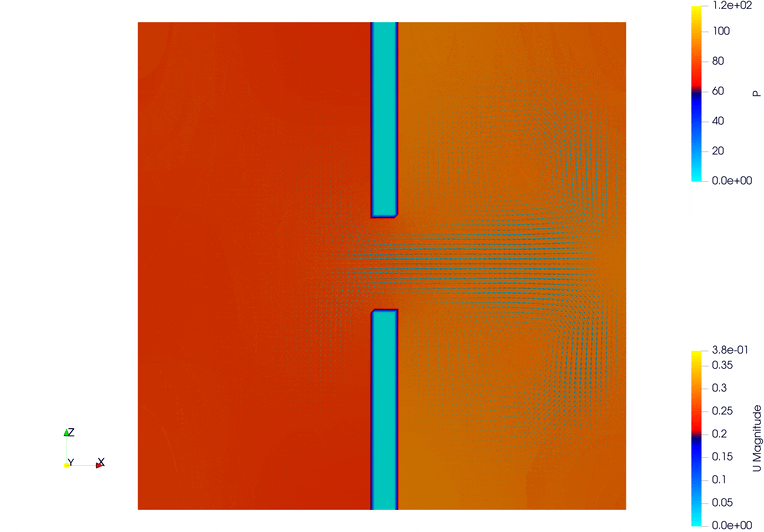
5.6. Pressure-Driven Flow Through Complex Geometry
This simulation demonstrates pressure-driven flow across a complex internal structure using the Lattice Boltzmann Method (LBM). The domain is discretized with a resolution of 400×400×400, offering fine detail of the flow field. Periodic boundary conditions are applied along the Y axis, and the X and Z axes remain non-periodic.
do_domain:
- domain:
bounds: [ [0,0,0] , [0.1,0.1,0.1] ]
grid_dims: [ 400 , 400 , 400 ]
periodic: [false, true, false ]
No external force is applied (Fext = [0,0,0]), and the kinematic viscosity is set to 1e-4.
set_lbm_parameters:
- lbm_parameters:
Fext: [0,0,0]
nuth: 1e-4
Pre-streaming boundary conditions include bounce-back on all walls and user-defined internal walls:
pre_stream_bcs:
- pre_bounce_back
- wall_bounce_back
A complex system of internal obstacles (walls) is defined to create a tortuous path for the flow. These walls are strategically placed along the X axis to create narrow channels and mixing zones.
set_obstacles:
- set_wall:
bounds: [[0.024,0,0.06],[0.026,0.1,0.1]]
- set_wall:
bounds: [[0.024,0,0],[0.026,0.1,0.04]]
- set_wall:
bounds: [[0.034,0,0.025],[0.036,0.1,0.075]]
- set_wall:
bounds: [[0.049,0,0.06],[0.051,0.1,0.1]]
- set_wall:
bounds: [[0.049,0,0],[0.051,0.1,0.04]]
- set_wall:
bounds: [[0.068,0,0.0355],[0.072,0.1,0.065]]
- set_wall:
bounds: [[0.085,0,0.02],[0.1,0.1,0.03]]
- set_wall:
bounds: [[0.085,0,0.07],[0.1,0.1,0.08]]
A high-density initialization is imposed on the far left of the domain using init_distributions with a tmp_coeff of 1.5. This sets up a large pressure difference that drives the fluid flow.
set_distributions:
- init_distributions:
tmp_coeff: 1.5
bounds: [[0,0,0], [0.024,1,1]]
Post-streaming bounce-back is applied to maintain no-slip conditions at the boundaries:
post_stream_bcs:
- post_bounce_back
